How to Derive Marshallian Demand Function

DIRECT UTILITY FUNCTION

Maximize U(X,Y) = ln(A) + αln(X)+ (1-α)ln(Y) Subject to PxX + PyY = I.
Solve the Marshallian demand function

How to Solve?
Step:

1. Do the Lagrange as below. (L =  ln(A) + αln(X)+ (1-α)ln(Y) -  [PxX + PyY - I].
2. Differentiate X, then find Lambda(Equation 1).
3. Differentiate Y, then find Lambda(Equation 2).
4. Differentiate Lambda(Equation 3).
5. Combine the both equation 1 and 3, then you can find whether X or Y. (Equation 4)
6. The X that you get in step 5 (equation 4), then substitute in equation equation 3. Then you will Y (Y Marshallian). 
7. After that substitute Y in equation in equation 4 to find X (X Marshallian)

Marshallian demand function

Maximize U(X,Y) = Subject to PxX + PyY = I.

Solve the Marshallian demand function. 

Marshallian demand function

Direct Utility Function

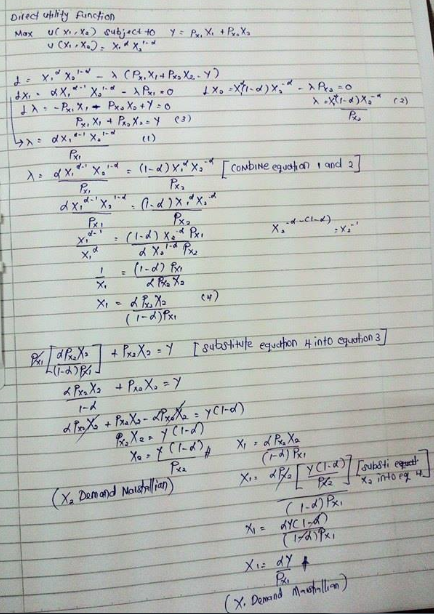Marshallian Demand Functon